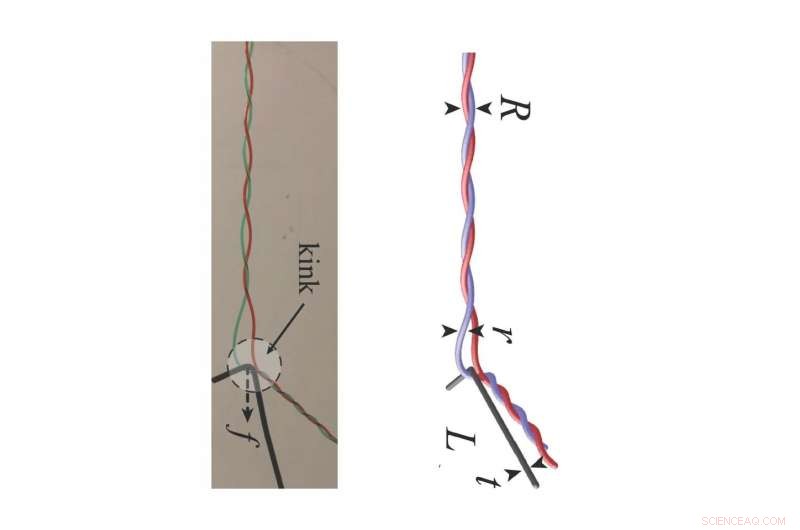
Experiment och simuleringar visar att pinnen rör sig längs den dubbla helixen från den fastklämda änden mot den fria änden. Kredit:Harvard SEAS
Som alla som någonsin har behövt borsta långt hår vet är knutar en mardröm. Men med tillräckligt med erfarenhet lär sig de flesta knepen med att reda ut med minsta möjliga smärta – börja längst ner, arbeta dig upp till hårbotten med korta, skonsamma borstar och applicera detangler vid behov.
L. Mahadevan, Lola England de Valpine-professorn i tillämpad matematik, i organisk och evolutionär biologi och i fysik, lärde sig kamningens mekanik för flera år sedan när han borstade sin unga dotters hår.
"Jag minns att spray som lossnar från trassel verkade fungera ibland, men jag måste fortfarande vara försiktig med att kamma försiktigt, genom att börja från de fria ändarna", sa Mahadevan. "Men jag fick snart sparken från jobbet eftersom jag inte var särskilt tålmodig."
Medan Mahadevan förlorade sin roll som frisör, var han fortfarande vetenskapsman och topologin, geometrin och mekaniken för dettangling ställde intressanta matematiska frågor som är relevanta för en rad applikationer inklusive textiltillverkning och kemiska processer som polymerbearbetning.
I en ny artikel, publicerad i tidskriften Soft Matter, Mahadevan och medförfattarna Thomas Plumb Reyes och Nicholas Charles, utforskar matematiken kring kamning och förklarar varför borstningstekniken som används av så många är den mest effektiva metoden för att reda ut ett knippe fibrer.
För att förenkla problemet simulerade forskarna två spiralformigt sammanflätade filament, snarare än ett helt hårstrå.
"Med hjälp av den här minimala modellen studerar vi redaktionen av den dubbla helixen via en enda styv pinne som rör sig längs den, och lämnar två orentrasslade filament i dess spår", säger Plumb-Reyes, doktorand vid SEAS. "Vi mätte krafterna och deformationerna i samband med kamning och simulerade det sedan numeriskt."
"Korta drag som börjar vid den fria änden och rör sig mot den fastklämda änden tar bort trassel genom att skapa ett flöde av en matematisk storhet som kallas "länktätheten" som kännetecknar mängden hårstrån som flätas med varandra, i enlighet med simuleringar av process", säger Nicholas Charles, doktorand vid SEAS.
Forskarna identifierade också den optimala minimilängden för varje slag – vilken som helst mindre och det skulle ta en evighet att kamma ut alla härvor och längre och det skulle vara för smärtsamt.
De matematiska principerna för borstning som utvecklats av Plumb-Reyes, Charles och Mahadevan användes nyligen av professor Daniela Rus och hennes team vid MIT för att designa algoritmer för att borsta hår med en robot.
Därefter siktar teamet på att studera mekaniken i att borsta lockigt hår och hur det reagerar på fukt och temperatur, vilket kan leda till en matematisk förståelse av ett faktum som varje person med lockigt hår känner till:borsta aldrig torrt hår.