
Bakhshali manuskript. Kredit:Bodleian Libraries, Oxfords universitet
Det borde inte komma som någon överraskning att den första registrerade användningen av siffran noll, upptäcktes nyligen vara gjorda så tidigt som på 300- eller 400-talet, hände i Indien. Matematik på den indiska subkontinenten har en rik historia som går tillbaka över 3, 000 år och blomstrade i århundraden innan liknande framsteg gjordes i Europa, med dess inflytande under tiden spridning till Kina och Mellanöstern.
Förutom att ge oss konceptet noll, Indiska matematiker gjorde viktiga bidrag till studiet av trigonometri, algebra, aritmetiska och negativa tal bland andra områden. Kanske viktigast, det decimalsystem som vi fortfarande använder världen över idag sågs först i Indien.
Talsystemet
Så långt tillbaka som 1200 f.Kr. matematisk kunskap skrevs ner som en del av en stor mängd kunskap som kallas Veda. I dessa texter, tal uttrycktes vanligtvis som kombinationer av tiopotenser. Till exempel, 365 kan uttryckas som tre hundra (3x10²), sex tior (6x10¹) och fem enheter (5x10⁰), även om varje potens av tio representerades med ett namn snarare än en uppsättning symboler. Det är rimligt att tro att denna representation med tiopotenser spelade en avgörande roll i utvecklingen av decimalvärdesystemet i Indien.
Från det tredje århundradet f.Kr. vi har också skriftliga bevis på Brahmi-siffrorna, föregångarna till det moderna, Indiskt eller hindu-arabiskt siffersystem som större delen av världen använder idag. När noll infördes, nästan all matematisk mekanik skulle vara på plats för att göra det möjligt för forntida indianer att studera högre matematik.
Konceptet noll
Zero i sig har en mycket längre historia. De nyligen daterade första inspelade nollorna, i vad som är känt som Bakhshali-manuskriptet, var enkla platshållare – ett verktyg för att skilja 100 från 10. Liknande märken hade redan setts i den babyloniska och mayakulturen under de tidiga århundradena e.Kr. och förmodligen i den sumeriska matematiken så tidigt som 3000-2000 f.Kr.
Men bara i Indien utvecklades platshållarsymbolen för ingenting till att bli en egen siffra. Tillkomsten av begreppet noll gjorde att tal kunde skrivas effektivt och tillförlitligt. I tur och ordning, detta möjliggjorde effektiv journalföring som innebar att viktiga finansiella beräkningar kunde kontrolleras retroaktivt, säkerställa ärliga handlingar från alla inblandade. Noll var ett viktigt steg på vägen till demokratisering av matematik.
Dessa tillgängliga mekaniska verktyg för att arbeta med matematiska begrepp, i kombination med en stark och öppen skolastisk och vetenskaplig kultur, menade det, omkring 600 e.Kr. alla ingredienser var på plats för en explosion av matematiska upptäckter i Indien. I jämförelse, dessa typer av verktyg populariserades inte i västerlandet förrän i början av 1200-talet, fast Fibonnaccis bok liber abaci.
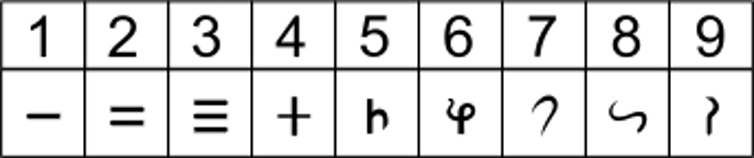
Brahmi-siffror. Kredit:Wikimedia
Lösningar av andragradsekvationer
På sjunde århundradet, det första skriftliga beviset på reglerna för att arbeta med noll formaliserades i Brahmasputha Siddhanta. I sin framstående text, Astronomen Brahmagupta introducerade regler för att lösa andragradsekvationer (så älskad av gymnasieelever i matematik) och för att beräkna kvadratrötter.
Regler för negativa tal
Brahmagupta visade också regler för att arbeta med negativa tal. Han hänvisade till positiva siffror som förmögenheter och negativa siffror som skulder. Han skrev ner regler som:"En förmögenhet subtraherad från noll är en skuld, " och "en skuld subtraherad från noll är en förmögenhet".
Detta senare uttalande är samma som regeln vi lär oss i skolan, att om du subtraherar ett negativt tal, det är samma sak som att lägga till ett positivt tal. Brahmagupta visste också att "Produkten av en skuld och en förmögenhet är en skuld" - ett positivt tal multiplicerat med ett negativt är ett negativt tal.
För den stora delen, Europeiska matematiker var ovilliga att acceptera negativa tal som meningsfulla. Många ansåg att negativa siffror var absurda. De resonerade att siffror utvecklades för att räkna och ifrågasatte vad man kunde räkna med negativa tal. Indiska och kinesiska matematiker insåg tidigt att ett svar på denna fråga var skulder.
Till exempel, i ett primitivt jordbrukssammanhang, om en bonde är skyldig en annan bonde 7 kor, då har den första bonden i praktiken -7 kor. Om den första bonden går ut för att köpa några djur för att betala tillbaka sin skuld, han måste köpa 7 kor och ge dem till den andra bonden för att få tillbaka hans kotal till 0. Från och med då, varje ko han köper går till hans positiva totalsumma.
Grund för kalkyl
Denna ovilja att anta negativa siffror, och faktiskt noll, höll europeisk matematik tillbaka i många år. Gottfried Wilhelm Leibniz var en av de första européerna som använde noll och de negativa på ett systematiskt sätt i sin utveckling av kalkyl i slutet av 1600-talet. Calculus används för att mäta förändringshastigheter och är viktig inom nästan alla vetenskapsgrenar, som särskilt underbygger många viktiga upptäckter inom modern fysik.
Men den indiska matematikern Bhāskara hade redan upptäckt många av Leibniz idéer över 500 år tidigare. Bhāskara, också gjort stora bidrag till algebra, aritmetisk, geometri och trigonometri. Han gav många resultat, till exempel om lösningarna av vissa "doifantinska" ekvationer, som inte skulle återupptäckas i Europa på århundraden.
Kerala skolan för astronomi och matematik, grundades av Madhava av Sangamagrama på 1300-talet, var ansvarig för många nybörjar i matematik, inklusive användning av matematisk induktion och några tidiga kalkylrelaterade resultat. Även om inga systematiska regler för kalkyl utvecklades av Kerala-skolan, dess förespråkare tänkte först på många av de resultat som senare skulle upprepas i Europa, inklusive Taylor-seriens expansioner, infinitessimaler och differentiering.
Språnget, tillverkad i Indien, som förvandlade noll från en enkel platshållare till en siffra i sig indikerar den matematiskt upplysta kultur som blomstrade på subkontinenten i en tid då Europa var fast i den mörka medeltiden. Även om dess rykte lider av den eurocentriska fördomen, subkontinenten har ett starkt matematiskt arv, som den fortsätter in på 2000-talet genom att tillhandahålla nyckelspelare i framkanten av varje gren av matematiken.
Denna artikel publicerades ursprungligen på The Conversation. Läs originalartikeln. 