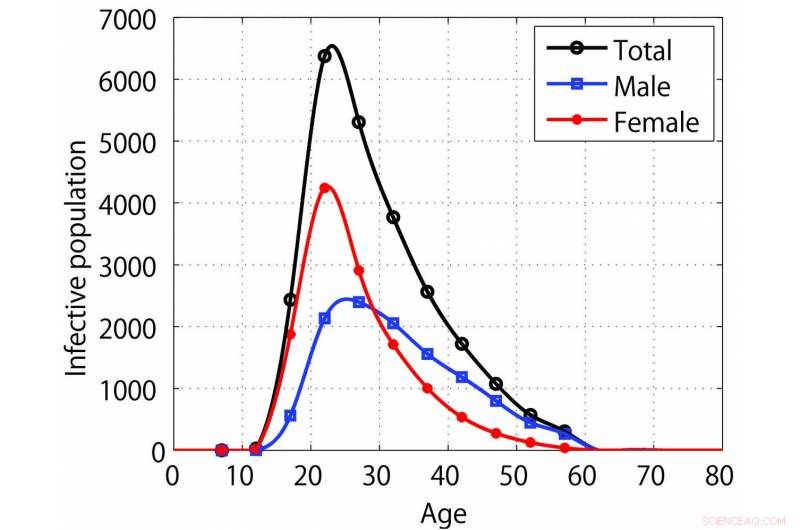
Interpolation av åldersfördelningar av rapporterade fall av klamydia i Japan 2015. Kredit:Toshikazu Kuniya, SIAM Journal on Applied Mathematics .
Matematiska modeller som kvantifierar dynamiken i infektionssjukdomar är avgörande prediktiva verktyg för kontroll av pågående och framtida utbrott. En infektions grundläggande reproduktionsnummer (R 0 ) är särskilt viktigt för sjukdomsmodellering och epidemiologi, eftersom det bestämmer globalt beteende och mäter en sjukdoms överförbarhet inom en fullt mottaglig population. Kortfattat, R 0 hjälper folkhälsotjänstemän att urskilja en epidemis intensitet och sannolikheten för framgångsrik spridning. Om R 0 > 1, ett utbrott inträffar. Om R 0 <1, infektionen dör vanligtvis ut.
Ibland är en sjukdom endemisk, vilket innebär att det kontinuerligt finns och upprätthålls på en baslinjenivå på en specifik plats. I dessa fall, antalet smittsamma individer förblir nästan statiskt och i endemisk jämvikt. klamydia, en sexuellt överförbar sjukdom hos både män och kvinnor som kan orsaka betydande skada på en kvinnas reproduktionssystem, har varit endemisk i Japan sedan 2012. För att matematiskt uppskatta R 0 för klamydias genomträngning i Japan, man måste klargöra stabiliteten i motsvarande modells endemiska jämvikt.
I en artikel som publicerades den 19 februari i SIAM Journal on Applied Mathematics , en publikation av Society for Industrial and Applied Mathematics, Toshikazu Kuniya studerar det globala beteendet hos en multigrupps SIR-epidemimodell med åldersstruktur och använder modellen för att uppskatta R 0 för Japans klamydiautbrott. Kuniya har modellerat infektionssjukdomar sedan han var masterstudent och är särskilt nyfiken på deras globala beteende. "Jag har nyligen blivit intresserad av tillämpningen av epidemimodeller på deras epidemiologiska överväganden, ", sa han. "Jag tror att epidemimodellernas globala beteende spelar en viktig roll för att förstå data om infektionssjukdomar på lång tid."
En SIR-modell – som står för känslig, smittsam, och återhämtat sig – är en enkel kompartmentmodell och en av de mest grundläggande mekanismerna för matematisk epidemiologi. Den delar upp den totala befolkningen i ett drabbat område i de tre ovannämnda klasserna. Denna typ av modell konvergerar till en sjukdomsfri jämvikt när R 0 <1 och en endemisk jämvikt när R 0 > 1.
Medan Kuniyas modell är ganska lik en som tidigare forskare använt, Kuniya formaterar om den till en multigruppsmodell med åldersberoende mottaglighet. "Jag valde en multigrupps SIR-epidemimodell med åldersstruktur eftersom det är användbart att hantera data med heterogenitet (kön, ålder, placera, etc.) för varje person, ", sa han. "Åldersstrukturen gör det möjligt för oss att överväga effekterna av den demografiska åldersfördelningens tidsvariation och åldersberoendet för varje epidemiparameter."
För enkelhetens skull, Kuniya antar att summan av dödligheten och återhämtningsgraden är konstant. Han försvagar också några av den tidigare modellens restriktiva antaganden som förhindrade framgångsrik tillämpning. "Under det tidigare antagandet, sjukdomsöverföringskoefficienten var oberoende av tillståndet hos smittsamma individer, " Sa Kuniya. "I den här studien, vi har försvagat detta antagande för att kunna överväga sjukdomsöverföringskoefficientens eventuella beroende av tillståndet hos smittsamma individer. På grund av detta, vi kan modellera sjukdomsöverföringen från manliga individer till kvinnliga individer och vice versa." Genom att göra det kan han bevisa att R 0 helt bestämmer modellens globala beteende. Det eliminerar också möjligheten för en instabil endemisk jämvikt om R 0 > 1.
Efter att ha etablerat sin modell, Kuniya tillämpar det på 2015 års manifestation av klamydia i Japan, för vilka det finns en tillgänglig heterogen datauppsättning ordnad efter ålder och kön. Klamydias till synes endemiska tillstånd de senaste åren gjorde också sjukdomen till ett lämpligt mål. Kuniya undersöker fyra särskilda fall - i form av en homogen modell, en åldersoberoende tvåkönsmodell, en åldersberoende enkönsmodell, och en åldersberoende tvåkönsmodell – och jämför de uppskattade resultaten av R 0 . Dessa specialfall ger ett R 0 uppskattning mellan 1,0148 och 1,0535 för klamydia i Japan. Hans analys avslöjar också att införandet av en åldersstruktur påverkar värdet av R 0 starkare än tillämpning av en tvågruppsstruktur. Detta indikerar att vanliga differentialekvationsmodeller som saknar åldersstruktur – även om de vanligtvis är lättare att använda än partiella differentialekvationsmodeller med åldersstruktur – i slutändan kan underskatta R 0 .
Under hela sin utredning, Kuniya antar att alla smittade individer är dokumenterade, när i verkligheten vissa förekomster av klamydia sannolikt inte rapporteras – särskilt eftersom sjukdomen ofta inte visar några symtom. Denna diskrepans kan ha lett till underskattad R 0 värden för de fyra enskilda fallen. Att redovisa orapporterade fall och förbättra uppskattningens övergripande noggrannhet är en uppgift för kommande studie.
I framtiden, Kuniya hoppas kunna tillämpa sina resultat på mer allmänna modeller med mer än två grupper, vilket kräver en allt mer utarbetad datauppsättning. "Jag tror att vi kan förbättra uppskattningen av R 0 och andra epidemiparametrar genom att använda en mer detaljerad datauppsättning uppdelad i enlighet med heterogeniteten - till exempel, sexuell aktivitet – av varje individ, " sa han. "Vi kan tillämpa våra teoretiska resultat på mer allmänna fall med godtyckliga antal grupper."