
Om du tyckte att multiplikationstabeller i skolan var svåra, föreställ dig att multiplicera tal med miljarder siffror. Kredit:Shutterstock/Nina Buday
Multiplikation av två tal är lätt, höger?
I grundskolan lär vi oss hur man gör lång multiplikation så här:
Metoder liknande detta går tillbaka tusentals år, åtminstone för de gamla sumererna och egyptierna.
Men är detta verkligen det bästa sättet att multiplicera två stora tal tillsammans?
I lång multiplikation, vi måste multiplicera varje siffra i det första talet med varje siffra i det andra talet. Om de två siffrorna vardera har N siffror, det är N 2 (eller N x N ) multiplikationer totalt. I exemplet ovan, N är 3, och vi fick göra 3 2 =9 multiplikationer.
Omkring 1956, den berömda sovjetiske matematikern Andrey Kolmogorov förmodade att detta är bästa möjliga sätt att multiplicera två tal tillsammans.
Med andra ord, oavsett hur du ordnar dina beräkningar, mängden arbete du måste göra kommer att vara proportionell mot åtminstone N 2 . Dubbelt så många siffror betyder fyra gånger så mycket arbete.
Kolmogorov kände att om en genväg var möjlig, det skulle säkert redan ha upptäckts. Trots allt, människor har multiplicerat siffror i tusentals år.
Detta är ett utmärkt exempel på den logiska felslutning som kallas "argumentet från okunnighet".
Ett snabbare sätt
Bara några år senare, Kolmogorovs gissning visade sig vara spektakulärt felaktig.
1960, Anatoly Karatsuba, en 23-årig matematikstudent i Ryssland, upptäckte ett lömskt algebraiskt trick som minskar antalet multiplikationer som behövs.
Till exempel, att multiplicera fyrsiffriga tal, istället för att behöva 4 2 =16 multiplikationer, Karatsubas metod kommer undan med bara nio. När han använder hans metod, dubbelt så många siffror betyder bara tre gånger så mycket arbete.
Detta blir en imponerande fördel när siffrorna blir större. För tal med tusen siffror, Karatsubas metod behöver cirka 17 gånger färre multiplikationer än lång multiplikation.
Men varför i hela friden skulle någon vilja multiplicera så stora tal tillsammans?
Faktiskt, det finns ett enormt antal ansökningar. En av de mest synliga och ekonomiskt betydelsefulla är inom kryptografi.
Stora siffror i verkligheten
Varje gång du engagerar dig i krypterad kommunikation på internet, till exempel, gå in på din bankwebbplats eller gör en webbsökning – din enhet utför ett stort antal multiplikationer, involverar siffror med hundratals eller till och med tusentals siffror.
Mycket troligt använder din enhet Karatsubas trick för denna aritmetik. Allt detta är en del av det fantastiska mjukvaruekosystemet som gör att våra webbsidor laddas så snabbt som möjligt.
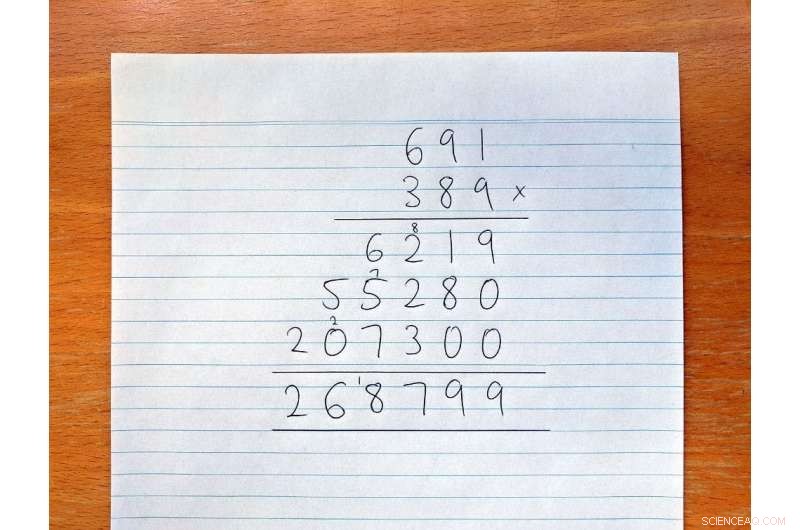
Den långa vägen till multiplikation. Kredit:David Harvey
För några mer esoteriska tillämpningar, matematiker måste hantera ännu större tal, med miljoner, miljarder eller till och med biljoner siffror. För sådana enorma antal, även Karatsubas algoritm är för långsam.
Ett verkligt genombrott kom 1971 med de tyska matematikerna Arnold Schönhages och Volker Strassens arbete. De förklarade hur man använder den nyligen publicerade snabba Fourier-transformen (FFT) för att multiplicera enorma tal effektivt. Deras metod används rutinmässigt av matematiker idag för att hantera tal i miljarder siffror.
FFT är en av 1900-talets viktigaste algoritmer. En applikation som är bekant i det dagliga livet är digitalt ljud:när du lyssnar på MP3, musikströmningstjänster eller digitalradio, FFT:er hanterar ljudavkodningen bakom kulisserna.
Ett ännu snabbare sätt?
I deras tidning från 1971, Schönhage och Strassen gjorde också en slående gissning. Att förklara, Jag måste bli lite teknisk ett tag.
Den första hälften av deras gissningar är att det ska vara möjligt att multiplicera N -siffriga siffror med ett antal grundläggande operationer som är proportionell mot högst N logg ( N ) (det vill säga N gånger den naturliga logaritmen för N ).
Deras egen algoritm nådde inte riktigt detta mål; de var för långsamma med en faktor log (log N ) (logaritmen för logaritmen av N ). Ändå, deras intuition fick dem att misstänka att de saknade något, och det N logg ( N ) bör vara genomförbart.
Under decennierna sedan 1971, ett fåtal forskare har hittat förbättringar av Schönhage och Strassens algoritm. I synnerhet, en algoritm designad av Martin Fürer 2007 kom plågsamt nära det svårfångade N logg ( N ).
Den andra (och mycket svårare) delen av deras gissningar är det N logg ( N ) bör vara den grundläggande hastighetsgränsen - att ingen möjlig multiplikationsalgoritm skulle kunna göra bättre än så här.
Låter bekant?
Har vi nått gränsen?
Några veckor sedan, Joris van der Hoeven och jag publicerade en forskningsartikel som beskrev en ny multiplikationsalgoritm som äntligen når N logg ( N ) helig gral, därmed lösa den "enkla" delen av Schönhage–Strassen-förmodan.
Tidningen har ännu inte granskats, så viss försiktighet är berättigad. Det är praxis inom matematik att sprida forskningsresultat innan de har genomgått peer review.
Istället för att använda endimensionella FFT - basen i allt arbete med detta problem sedan 1971 - bygger vår algoritm på flerdimensionell FFTs. Dessa prylar är inget nytt:det flitigt använda JPEG-bildformatet beror på 2-dimensionella FFT, och 3-dimensionella FFT:er har många tillämpningar inom fysik och teknik.
I vår tidning, vi använder FFTs med 1, 729 dimensioner. Det här är svårt att visualisera, men matematiskt sett inte mer besvärligt än det 2-dimensionella fallet.
Verkligen, riktigt stora siffror
Den nya algoritmen är inte riktigt praktisk i sin nuvarande form, eftersom beviset som ges i vår tidning bara fungerar för löjligt stora antal. Även om varje siffra skrevs på en väteatom, det skulle inte finnas tillräckligt med utrymme i det observerbara universum för att skriva ner dem.
Å andra sidan, vi är hoppfulla att med ytterligare förbättringar, Algoritmen kan bli praktisk för tal med bara miljarder eller biljoner siffror. Om så är fallet, det kan mycket väl bli ett oumbärligt verktyg i beräkningsmatematikerns arsenal.
Om hela Schönhage–Strassen gissningen är korrekt, sedan ur en teoretisk synvinkel, den nya algoritmen är slutet på vägen – det går inte att göra bättre.
Personligen, Jag skulle bli mycket förvånad om gissningarna visade sig vara felaktiga. Men vi får inte glömma vad som hände med Kolmogorov. Matematik kan ibland skapa överraskningar.
Denna artikel publiceras från The Conversation under en Creative Commons -licens. Läs originalartikeln. 