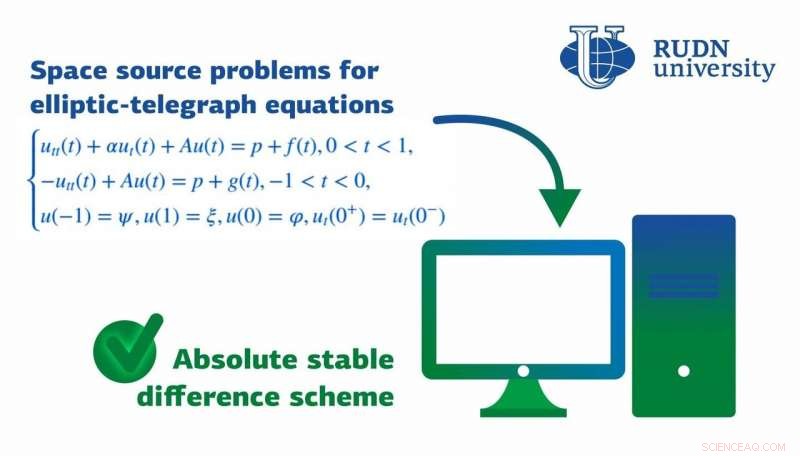
En matematiker från RUDN University föreslog ett stabilt skillnadsschema för att lösa omvända problem för elliptiska telegrafer och differentialekvationer som används för att beskriva biologiska, fysisk, och sociologiska processer. Resultaten av studien publicerades i Numeriska metoder för partiella differentialekvationer tidning.

Elliptiska ekvationer är en klass av differentialekvationer i partiella derivator som används, bland annat, att modellera tidsoberoende processer. Telegrafekvationer presenteras i en icke-stationär form. De erhölls ursprungligen för en telegrafkommunikationslinje, men idag används de också för att modellera insekters rörelser, blodflödet genom venerna, och de förändringar som byggmaterial genomgår. Dessutom, de kan omvändas, d.v.s. används för att hitta en källa till förändringar baserat på kända processegenskaper, till exempel, för att identifiera en orsak till materiell skada eller för att skapa en optisk tomografibild för medicinsk diagnostik. Det är ofta svårt att få exakta lösningar på problem som dessa; därför, det initiala problemet reduceras till ett system av enklare ekvationer som ger ett svar med en viss grad av approximation till det korrekta. En matematiker från RUDN University föreslog en algoritm för att få omvända problemlösningar för elliptiska telegrafekvationer med hjälp av en dator.

"Ju mer komplext ett modellerat system, ju mer okända parametrar den innehåller, och desto svårare är beräkningarna. Dock, trots uppgiftens komplexitet, moderna datorer kan användas för att söka efter ungefärliga lösningar på differentialekvationer. Vi strävade efter att erhålla absoluta stabila skillnadsscheman för den ungefärliga lösningen av rymdidentifieringsproblemet för elliptiska telegrafekvationer. Vårt arbete kan hjälpa till att implementera dessa metoder ytterligare i modelleringen av olika processer, " sade prof. Allaberen Ashyralyev, en Ph.D. i fysik och matematik från institutionen för högre matematik, RUDN universitet.

Ett sätt att få en ungefärlig lösning är att ersätta det ursprungliga problemet med differensscheman. Det studerade området förvandlas till ett rutnät med en given stegstorlek, och funktioner ersätts med nodvärden. Matematikern föreslog ett skillnadsschema och studerade det sedan både analytiskt och numeriskt. Den första metoden användes för att bekräfta schemats absoluta stabilitet, och det andra (ett numeriskt experiment, d.v.s. en ekvation som schemat tillämpades på)—för att stödja resultaten av analysen. Forskaren lyckades visa att schemat var absolut stabilt och oberoende av den valda beräkningsstegstorleken.

"Liknande elliptiska telegrafekvationer används för att modellera biologiska system, sociologiska fenomen, och tekniska processer. Ett absolut stabilt skillnadsschema kan hjälpa specialister att bättre studera dessa frågor, " tillade Prof. Allaberen Ashyralyev från RUDN University.