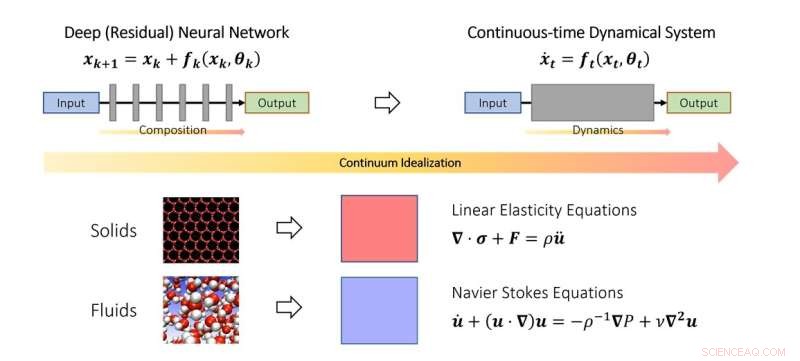
Den kontinuerliga synen på djupt lärande. I likhet med hur forskare studerar fast- och vätskemekanik i kontinuumgränsen, kan man också idealisera djupa neurala nätverk som en diskretisering av ett kontinuerligt dynamiskt system. I schemat representerar den fiktiva tidsparametern en kontinuerlig analog av lager och dynamiken modellerar lagerstaplingen. Kredit:Qianxiao Li
NUS-matematiker har utvecklat ett nytt teoretiskt ramverk baserat på dynamiska system för att förstå när och hur ett djupt neuralt nätverk kan lära sig godtyckliga samband.
Trots att man uppnått stor framgång i praktiken är det fortfarande en utmanande uppgift att förstå de teoretiska principerna för djupinlärning. En av de mest grundläggande frågorna är:kan djupa neurala nätverk lära sig godtyckliga input-output-relationer (i matematik kallas dessa funktioner), och skiljer sig sättet att uppnå detta från traditionella metoder?
För att förstå denna fråga är det nödvändigt att tänka på exakt vad som är nytt i djupa neurala nätverk jämfört med traditionella funktionsapproximationsparadigm. Till exempel, klassisk Fourier-serie approximerar komplicerade funktioner som en viktad summa av enklare funktioner, såsom sinus och cosinus. Djupa neurala nätverk fungerar helt annorlunda. Istället för viktade summor bygger de komplexa funktioner ur den upprepade staplingen av enkla funktioner (lager). Detta är också känt som funktionssammansättning i matematik. Nyckelfrågan är hur komplicerade funktioner kan byggas av enkla genom att stapla dem ihop. Det visar sig att detta är ett ganska nytt problem inom den gren av matematik som kallas approximationsteori.
I denna studie publicerad i Journal of the European Mathematical Society , biträdande professor Qianxiao LI från Institutionen för matematik, National University of Singapore och hans medarbetare utvecklade en ny teori om approximationsförmåga för funktionssammansättning. En intressant observation är att även om funktionssammansättning är utmanande att analysera i praktiken på grund av dess diskreta och olinjära struktur, är det inte första gången det finns sådana problem.
I studien av fasta ämnens och vätskors rörelse idealiseras de ofta som ett kontinuum av partiklar, som uppfyller vissa kontinuerliga ekvationer (vanliga eller partiella differentialekvationer). Detta gör att svårigheten att modellera sådana system på den diskreta atomnivån kan kringgås. Istället härleddes kontinuumekvationer som modellerar deras beteende på makroskopisk nivå.
Nyckeltanken i studien är att detta koncept kan utvidgas till djupa neurala nätverk, genom att idealisera den skiktade strukturen som ett kontinuerligt dynamiskt system. Detta förbinder djupinlärning med den gren av matematik som kallas dynamiska system. Sådana kopplingar möjliggör utveckling av nya verktyg för att förstå matematiken för djupinlärning, inklusive en allmän karakterisering av när det verkligen kan approximera godtyckliga samband.
Prof Li sa:"Deep learnings dynamiska systemsyn erbjuder ett lovande matematiskt ramverk som belyser de utmärkande aspekterna av djupa neurala nätverk jämfört med traditionella paradigm. Detta medför spännande nya matematiska problem i gränssnittet mellan dynamiska system, approximationsteori och maskininlärning. "
"Ett lovande område för framtida utveckling är att utöka detta ramverk för att studera andra aspekter av djupa neurala nätverk, till exempel hur man tränar dem effektivt och hur man säkerställer att de fungerar bättre på osynliga datauppsättningar," tillade Prof Li. + Utforska vidare