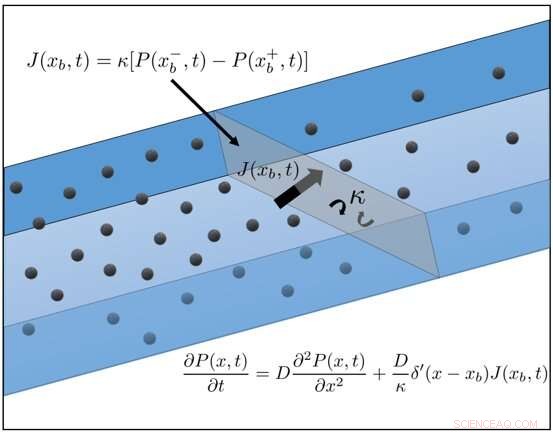
En banbrytande ny ekvation har utvecklats för att modellera diffusiv rörelse genom permeabelt material exakt för allra första gången. Kredit:University of Bristol
En banbrytande matematisk ekvation som skulle kunna förändra medicinska procedurer, naturgasutvinning och produktion av plastförpackningar i framtiden har upptäckts.
Den nya ekvationen, utvecklad av forskare vid University of Bristol, indikerar att diffusiv rörelse genom permeabelt material kan modelleras exakt för allra första gången. Det kommer ett sekel efter att världsledande fysiker Albert Einstein och Marian von Smoluchowski härledde den första diffusionsekvationen, och markerar viktiga framsteg när det gäller att representera rörelse för ett brett spektrum av enheter från mikroskopiska partiklar och naturliga organismer till konstgjorda enheter.
Hittills har forskare som tittar på partikelrörelser genom porösa material, såsom biologiska vävnader, polymerer, olika stenar och svampar, varit tvungna att förlita sig på approximationer eller ofullständiga perspektiv.
Resultaten publicerade idag i tidskriften Physical Review Research , tillhandahåller en ny teknik som ger spännande möjligheter i en mängd olika miljöer, inklusive hälsa, energi och livsmedelsindustrin.
Huvudförfattaren Toby Kay, som avslutar en doktorsexamen. i Engineering Mathematics, sade:"Detta markerar ett grundläggande steg framåt sedan Einstein och Smoluchowskis studier om diffusion. Det revolutionerar modelleringen av diffuserande enheter genom komplexa medier i alla skalor, från cellulära komponenter och geologiska föreningar till miljömässiga livsmiljöer.
"Tidigare har matematiska försök att representera rörelse genom miljöer utspridda med föremål som hindrar rörelse, så kallade permeabla barriärer, begränsats. Genom att lösa detta problem banar vi vägen för spännande framsteg inom många olika sektorer eftersom permeabla barriärer rutinmässigt stöter på av djur, cellulära organismer och människor."
Kreativitet i matematik tar sig olika uttryck och en av dessa är sambandet mellan olika nivåer av beskrivning av ett fenomen. I det här fallet, genom att representera slumpmässig rörelse på ett mikroskopiskt sätt och sedan zooma ut för att beskriva processen makroskopiskt, var det möjligt att hitta den nya ekvationen.
Ytterligare forskning behövs för att tillämpa detta matematiska verktyg på experimentella tillämpningar, vilket kan förbättra produkter och tjänster. Att till exempel kunna modellera diffusionen av vattenmolekyler genom biologisk vävnad kommer att främja tolkningen av diffusionsvägda MRI-avläsningar (Magnetic Resonance Imaging). Det skulle också kunna erbjuda en mer exakt representation av luftspridning genom livsmedelsförpackningsmaterial, vilket hjälper till att bestämma hållbarhet och föroreningsrisk. Dessutom kan kvantifiering av beteendet hos djur som söker föda som interagerar med makroskopiska barriärer, såsom staket och vägar, ge bättre förutsägelser om konsekvenserna av klimatförändringar i bevarandesyften.
Användningen av geolocatorer, mobiltelefoner och andra sensorer har sett spårningsrevolutionen generera rörelsedata av ständigt ökande kvantitet och kvalitet under de senaste 20 åren. Detta har visat på behovet av mer sofistikerade modelleringsverktyg för att representera rörelsen av vidsträckta enheter i deras miljö, från naturliga organismer till konstgjorda enheter.
Seniorförfattaren Dr. Luca Giuggioli, docent i komplexitetsvetenskap vid University of Bristol, sa:"Denna nya fundamentala ekvation är ytterligare ett exempel på vikten av att konstruera verktyg och tekniker för att representera diffusion när rymden är heterogen; det vill säga när den underliggande miljön förändras från plats till plats.
"Den bygger på en annan efterlängtad lösning 2020 av en matematisk gåta för att beskriva slumpmässiga rörelser i slutet utrymme. Den här senaste upptäckten är ytterligare ett viktigt steg framåt för att förbättra vår förståelse av rörelse i alla dess former och former – gemensamt kallad matematiken för rörelse – som har många spännande potentiella tillämpningar." + Utforska vidare