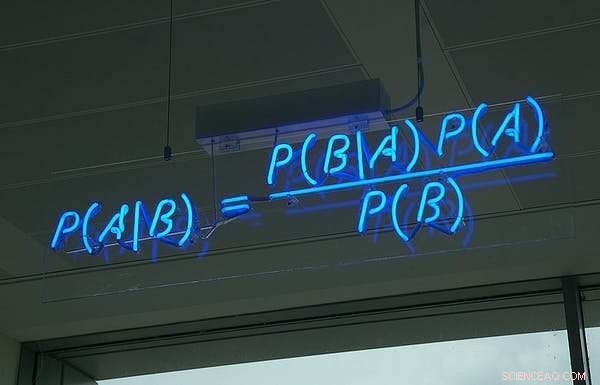
Bayes teorem, i neon, på det brittiska mjukvaruföretaget HP Autononys kontor. Kredit:Wikimedia Commons, CC BY
Australiens katastrofala översvämningar på östkusten har beskrivits av NSW:s premiärminister som en "en på 1 000-årig händelse, en term som har skapat en hel del förvirring.
Långa förklaringar om att dessa termer inte är samma som "förekommer med 1 000 års mellanrum" eller "en gång var 1 000 år" har bara ökat förvirringen.
Den enklaste förklaringen är att den faktiska innebörden av "en på 1 000 år" är "att ha en sannolikhet på 0,1 procent under ett givet år" (1 på 1 000), vilket väcker frågan:varför säger folk inte bara det?
Den främsta anledningen är att dessa termer går tillbaka till en tid då de flesta inte tänkte i termer av sannolikheter, och även de som gjorde det var förvirrade över hur de fungerade. Nuförtiden interagerar vi med sannolikheter hela tiden.
Den dagliga väderprognosen inkluderar en procentuell sannolikhet för regn, och långsiktiga prognoser ger sannolikheten för högre eller lägre nederbörd än genomsnittet enligt El Nino- och La Nina-cyklerna.
Finansmarknaderna satsar på sannolikheter eller ränterörelser. Statistik och sannolikhet lärs ut till barn i skolan.
Men detta är en ganska ny utveckling.
Fram till 1600-talet var även de mest elementära begreppen sannolikhetsteorin okända. Människor ansåg öde och förmögenhet som i huvudsak okända. Även spelare förstod inte odds.
Sannolikhetens födelse
Det var faktiskt en förfrågan från en gamblersvän omkring 1654 som motiverade den franske filosofen och matematikern Blaise Pascal att utveckla de grundläggande begreppen sannolikhet tillsammans med sin kollega Pierre de Fermat.
(Pascal använde också idén för att utveckla "Pascals satsning" som användes för att visa nyttan av att tro på Gud. Tanken är att om Gud existerar kommer de troende att belönas med evig salighet. Om inte, kommer de att avstå från ett begränsat antal jordiska nöjen medan levande. Oavsett hur liten sannolikheten för att Gud existerar, visar sig fördelen med att tro på Gud vara oändlig medan kostnaden är begränsad.)
Förståelsen utvecklades långsamt. Det var inte förrän i mitten av 1700-talet innan den engelske prästen Thomas Bayes fick kredit för områdets viktigaste utveckling.
Verktyget testamenterat av Bayes
I sin moderna tolkning ger Bayes teorem oss möjlighet att revidera vår syn på sannolikheten för en händelse i ljuset av bevis om vad som just har hänt.
Huruvida något just har hänt eller inte matas uttryckligen in i omräkningen tillsammans med uppdaterade bedömningar av sannolikheten att det spelar roll.
Fram till Bayes beräknades de flesta sannolikheter som om de var oföränderliga, till exempel sannolikheten att få "huvuden" när man kastade ett mynt. Dessa sannolikheter kan med fördel beskrivas som "en på 1 000 år" eller "i genomsnitt varannan kast."
Men sannolikheten för en allvarlig översvämning förändras över tiden i takt med att förhållandet mellan de komponenter som utgör vädersystemet förändras. Huruvida en översvämning har inträffat ger oss bevis på den förändringen.
Detta gör att det inte längre hjälper att hänvisa till en allvarlig översvämning som "en på x år".
Det är länge sedan vi ändrade terminologin en gång på så många år, men till vad? Svaret verkar enkelt, även om detaljerna kommer att vara knepiga.
Först måste vi omvandla de gamla måtten till allvarlighetsskalor, liknande de som används för cykloner och jordbävningar, men specifika för varje avrinningsområde.
Efter att ha gjort det kan sannolikheten för en händelse av given svårighetsgrad uppskattas på grundval av historisk erfarenhet och uppdateras i ljuset av nya bevis.
Hur skulle detta gälla i fallet med en händelse som Lismore-floden?
Den initiala "ett på 1 000 år"-beskrivningen betyder att en sådan händelse skulle vara extremt osannolik om det gamla förhållandet höll.
Med Bayes' teorem skulle vi uppdatera den initiala på 1 000 sannolikhet på basis av uppdaterad information om chansen att de underliggande sambanden förändras, vilket ger nya årliga sannolikheter varje år.
Så här fungerar maskininlärning och hur medicinska och försäkringsmässiga odds uppdateras. Tyvärr kommer de reviderade sannolikheterna nästan säkert att överstiga en av 1 000.