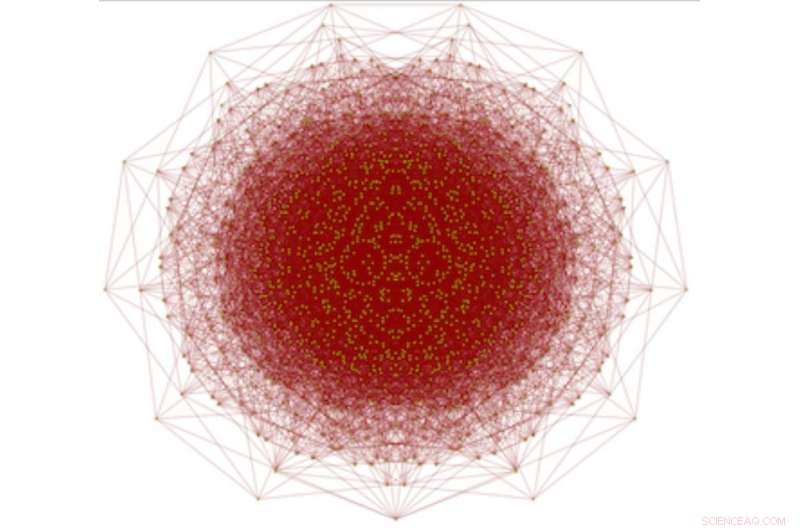
1581-vertexen, icke-4-färgbar enhetsavståndsgraf G. Kredit:arXiv:1804.02385 [math.CO]
Professionell biolog och amatörmatematiker Aubrey de Gray har delvis löst Hadwiger-Nelson-problemet, som har retat matematiker sedan 1950. Han har publicerat en artikel som beskriver lösningen på arXiv förtrycksserver.
Hadwiger-Nelson-problemet uppstod när Edward Nelson och Hugo Hadwiger undrade över det minsta antalet färger som behövs för att färga alla punkter på en graf, utan att två anslutna punkter använder samma färg. Över åren, matematiker har attackerat problemet, och har minskat möjligheterna till fyra, fem, sex eller sju. Nu, de Grey har eliminerat möjligheten med fyra färger som lösningen.
Intressant, de Gray är välkänd för sitt arbete inom sitt primära område, biologi. Mer specifikt, han har gjort offentliga kommentarer som tyder på att vissa människor som lever idag kommer att bli tusen år gamla på grund av begynnande medicinska genombrott. Han har etablerat en stiftelse dedikerad till att vända åldrandet och fortsätter att arbeta med problemet. Hans resa till matematik pussellösare, han noterar, har rötter i sin kärlek till spelet Othello. Han brukade vara en tävlingsspelare, genom vilken han blev vän med en grupp matematiker. De slutade lära honom lite matematikteori, som han började utforska som ett sätt att varva ner efter en hård dag på jobbet.
Flera år senare, en grupp matematiker satte ihop Polymath Project, ett samarbete mellan matematiker runt om i världen – deras onlineplattform gör att de som är intresserade av att arbeta med svåra matematikpussel kan samarbeta med likasinnade individer. Det var på den plattformen som de Gray hittade Hadwiger-Nelson-problemet. Han började arbeta på det under sin jullov, och efter att ha utforskat problemet med Moser-spindeln, upptäckte att ett av antagandena från tidigare matematiker var fel, och på grund av det, han kunde utesluta fyra färger som en möjlig lösning.
Amatörmatematikern tar dock inte sig själv på alltför stort allvar, han beskriver sina fynd som "extraordinärt lyckliga".
© 2018 Phys.org