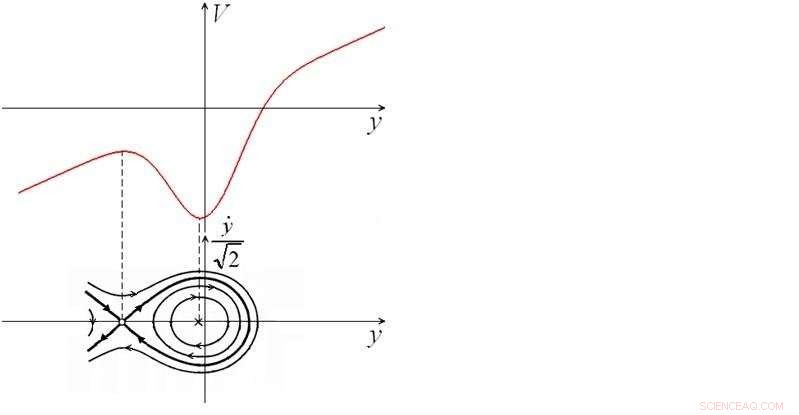
Fasbanor för ett socialt system i en konfliktsituation utan yttre störningar. Upphovsman:Lobachevsky University
Ett team av forskare under ledning av docent Alexander Petukhov vid Institute of International Relations and World History vid Lobachevsky University utvecklar modeller för sociala konflikter utifrån olinjär dynamik.
För matematisk modellering, ett viktigt inslag i sociala och politiska processer är att de inte kan definieras strikt. De är alltid föremål för små förändringar och fluktuationer. Ganska ofta, sociala processer jämförs med bruna partiklar. Dessa små förändringar (fluktuationer) i deras bana förklaras av andra molekylers kaotiska rörelse. I sociala processer, fluktuationer kan betraktas som manifestationer av deras enskilda deltagares fria vilja, liksom andra slumpmässiga manifestationer av den yttre miljön.
Inom fysiken, dessa processer beskrivs vanligtvis av Langevins stokastiska diffusionsekvation, som också har tillämpats för att modellera vissa sociala processer.
Metoden baserad på sådana ekvationer har flera fördelar:
Modellen bygger på tanken att individer interagerar i samhället genom ett kommunikationsfält - h. Detta fält, som skapas av varje individ i samhället, modellerar informationsinteraktionen mellan individer.
Dock, det bör förstås att detta är ett samhälle som knappast kan hänföras till ett objekt i klassisk fysisk rumslig topologi.
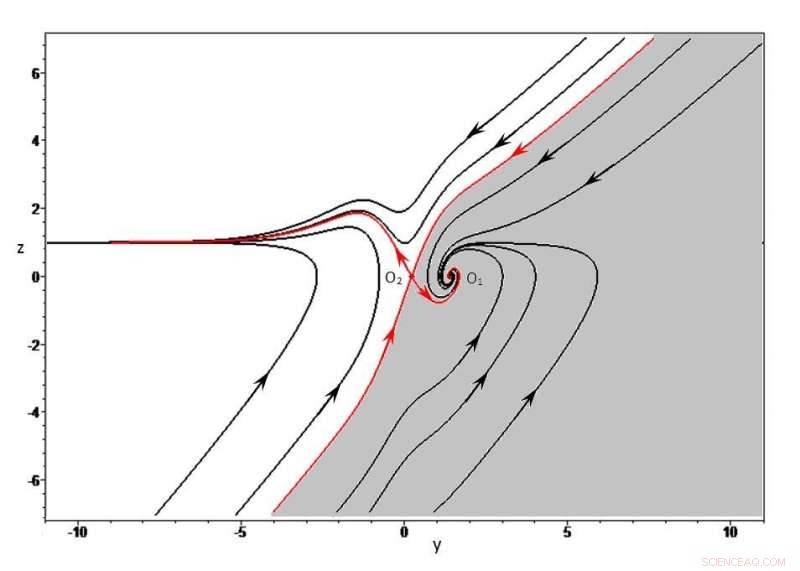
Fasbanor för ett socialt system i en konfliktsituation med yttre störningar. Upphovsman:Lobachevsky University
Enligt Dr Petukhov, ur informationsöverföring mellan individer, rymden i samhället kombinerar både klassiska rumsliga koordinater och ytterligare specifika funktioner. Detta förklaras av det faktum att i den moderna informationsvärlden, det finns ingen anledning att vara nära inflytandeobjektet för att förmedla information till detta objekt.
"Således, samhället är en flerdimensionell, socialt och fysiskt utrymme som återspeglar en individs förmåga att 'nå' en annan individ med sitt kommunikationsfält, det är, att påverka den personen, hans parametrar och förmåga att röra sig i ett visst utrymme, "konstaterar Alexander Petukhov.
Följaktligen, individens position i förhållande till andra individer i ett sådant utrymme ger en modell av nivån på förhållandet mellan dem och deras engagemang i informationsutbyte. När individer ligger nära varandra i den här modellen, det betyder att det sker ett regelbundet informationsutbyte mellan dem, och en social förbindelse har upprättats. I detta sammanhang, varianten av interaktion mellan individer eller grupper av individer som resulterar i en dramatisk ökning av avståndet (dvs. det sociala avståndet Δx =xi — xj, där x är koordinaten i det sociala och fysiska rummet, jag, j =[1, N], där N är antalet individer eller konsoliderade grupper av individer) mellan dem bör betraktas som en konflikt.
Därför, förutsatt att en individ liknar en brun partikel med en viss påverkningsradie på andra individer, kommunikationsfältet kan representeras med hjälp av diffusionsekvationen.
Baserat på den metod som presenteras ovan och modellen som utvecklats av forskare från Lobachevsky University, följande karakteristiska mönster och beroende av de initiala och gränsvillkoren avslöjades:
Det har också bevisats under dessa studier att övergången av ett distribuerat kognitivt system med flera komponenter från ett stabilt tillstånd till ett instabilt är en tröskeleffekt. Enligt Alexander Petukhov, experimenten utförda av forskare vid Lobachevsky -universitetet har avslöjat de specifika parametrar som krävs för att styra ett sådant system:De bestämmer övergången från ett stabilt tillstånd till ett instabilt, vilket gör det möjligt, med full kontroll över sådana parametrar, skapa förutsättningar för uppkomsten av en social konflikt, eller, tvärtom, för att förhindra det.
"Genom att utveckla detta tillvägagångssätt i framtiden, vi kommer på grundval av detta att kunna skapa ett verktyg för adekvat prognos av sociala konflikter ", Säger Alexander Petukhov.