Den 5 januari Rosa Winter kommer att doktorera i aritmetisk geometri. Hon forskade på lösningar av ekvationer som definierar så kallade 'del Pezzo-ytor." "Jag gillar geometri eftersom jag kan föreställa mig och rita formerna och föremålen, " säger Winter. "Det gör att abstrakt matematik känns mer påtaglig."

I matematik, det är ibland användbart att studera abstrakta ekvationer med hjälp av geometriska objekt, som cirklar, sfärer, oktaedrar, eller till och med högre dimensionella objekt. Fältet som förbinder geometri med abstrakta ekvationer kallas aritmetisk geometri. Ph.D. kandidat Rosa Winter tillämpade denna specifika typ av geometri i sin avhandling.

Ritytor

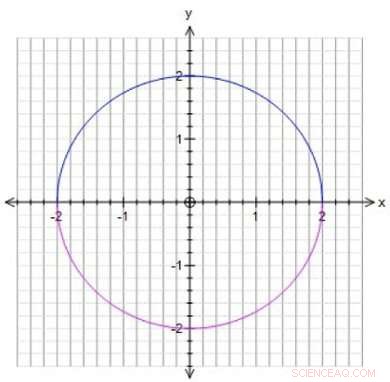
Matematiska ekvationer kan definiera geometriska objekt, vilket innebär att det är möjligt att studera lösningar på dessa ekvationer med hjälp av geometri. Till exempel, om du vill veta vilka siffror du kan ange för att göra x^2+y^2 lika med 4, du kan rita alla punkter (lösningar) för vilka x^2+y^2=4. Detta resulterar i en cirkel med radie 2, vilket visar, till exempel, att punkten x=2, y=0 är en lösning. Du kan också leta efter specifika lösningar, liknande punkter på cirkeln där x och y är bråk (1/3, 1/5:e, men också, 0, 2, etc.). Dessa bråklösningar kallas rationella punkter. Winter studerade rationella punkter på ytor. "Ytor är alltid tvådimensionella, även om de lever i åtta dimensioner, " säger Winter. "Vilket betyder att jag kan rita ytor, gör den abstrakta matematiken mer intuitiv för mig."

Miljonfråga

Att hitta rationella punkter på geometriska föremål är sällan lätt. Detta visas, till exempel, genom den så kallade "Birch and Swinnerton-Dyer-förmodan". Denna ännu obevisade matematiska gissning är en del av Millennium Prize Problems. Clay Mathematics Institute delar ut en miljon dollar till en korrekt lösning på något av dessa problem. Gissningen handlar om rationella punkter på elliptiska kurvor. Som cirklar, elliptiska kurvor är geometriska objekt som definieras av vissa ekvationer. När du ritar dem, de ser ut som böjda linjer. Vinter:"Även på elliptiska kurvor, som vi vet ganska mycket om, det är inte lätt att bestämma mängden rationella punkter."

Del Pezzo ytor

Tyvärr, Winter samlade inte in miljonen dollar under sin doktorsexamen. forskning. Hon arbetade inte på rationella punkter på elliptiska kurvor, men på så kallade 'del Pezzo-ytor av grad 1." Vinter:"Ur geometrisk synvinkel, dessa är inte de svåraste, mest komplicerade ytor men de innehåller fortfarande obesvarade matematiska frågor." Hon visade för en del av denna familj av ytor att den innehåller ett oändligt antal rationella punkter som inte klungar ihop sig; de kan hittas utspridda runt ytorna. Om rationella punkter var synliga som röda prickar och du kan gå över en sådan del-Pezzo-yta, du skulle se röda rationella punkter överallt du tittar.

Sedan september, Winter har arbetat som postdoc vid Max Planck Institute for Mathematics in the Sciences i Leipzig. Här lär hon sig bland annat, hur man tillämpar geometri och abstrakt matematik i andra vetenskaper, som biologi och fysik.