
Var olika sätt att lära ut operationsordningen ansvariga för förvirring? Kredit:Shutterstock
I ungefär ett decennium nu har matematiker och matematikpedagoger vägt in i en speciell debatt med rötter i skolmatematiken som inte visar några tecken på att avta.
Debatten, täckt av Slate, Popular Mechanics , The New York Times och många andra butiker, är fokuserad på en ekvation som blev så "viral" att den till slut klumpas ihop med andra fenomen som har "brutit" eller "delat" internet.
Om du ännu inte har vägt in, skulle det vara ett bra tillfälle att se var du står. Vänligen svara på följande:
8÷2(2+2)=?
Om du är som de flesta var ditt svar 16 och är förvånad över att någon annan kan hitta ett annat svar. Om du inte är som de flesta andra och ditt svar var 1 och du är lika förvirrad över att se det på ett annat sätt. Var inte rädd, i det följande kommer vi att förklara det definitiva svaret på denna fråga – och varför sättet som ekvationen skrivs på bör förbjudas.
Vårt intresse väcktes eftersom vi har forskat om konventioner om att följa operationsordningen – en sekvens av steg som tas när vi står inför en matematisk ekvation – och vi var lite förvirrade över vad allt väsen handlade om.
Svaret är uppenbarligen...
Två hållbara svar på ett matematiskt problem? Tja, om det är en sak vi alla kommer ihåg från mattelektionen:det kan inte stämma!
Många teman dök upp från uppsjön av artiklar som förklarade hur och varför denna "ekvation" slog sönder internet. Att skriva in uttrycket på miniräknare, av vilka några är programmerade att respektera en viss ordningsföljd, diskuterades mycket.
Andra, som säkrar lite, föreslår att båda svaren är korrekta (vilket är löjligt).
Det mest dominerande temat fokuserade helt enkelt på implementering av operationsordningen enligt olika akronymer. Vissa kommentatorer sa att människors missförstånd tillskrevs felaktig tolkning av den memorerade akronymen som lärs ut i olika länder för att komma ihåg operationsordningen som PEMDAS, som ibland används i USA:PEMDAS syftar på att tillämpa parenteser, exponenter, multiplikation, division, addition och subtraktion.
En person som följer denna ordning skulle få 8÷2(2+2) att bli 8÷2(4) tack vare att börja med parenteser. Sedan blir 8÷2(4) 8÷8 eftersom det inte finns några exponenter, och "M" står för multiplikation, så de multiplicerar 2 med 4. Slutligen, enligt "D" för division, får de 8÷8=1.
Däremot kan kanadensare läras att komma ihåg BEDMAS, som står för att tillämpa parenteser, exponenter, division, multiplikation, addition och subtraktion. Någon som följer denna ordning skulle få 8÷2(2+2) att bli 8÷2(4) tack vare att man börjar med parenteser (samma som parenteser). Sedan blir 8÷2(4) 4(4) eftersom (det finns inga exponenter) och "D" står för division. Slutligen, enligt "M" för multiplikation, 4(4)=16.
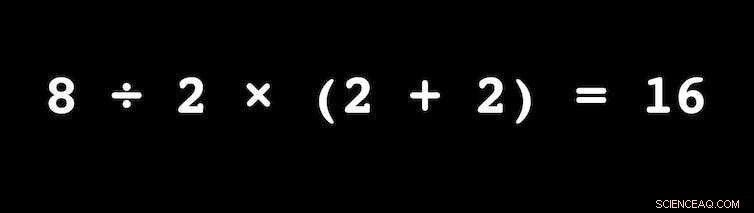
Hade problemet presenterats korrekt som 8 ÷ 2 × (2 + 2) =?, skulle det inte bli någon het debatt. Kredit:Egan J. Chernoff, författare tillhandahållen
Uteslut inte multiplikationssymbolen
För oss är uttrycket 8÷2(2+2) syntaktiskt fel.
Nyckeln till debatten, hävdar vi, är att multiplikationssymbolen före parentesen utelämnas.
Ett sådant utelämnande är en konvention inom algebra. Till exempel, i algebra skriver vi 2x eller 3a vilket betyder 2 × x eller 3 × a. När bokstäver används för variabler eller konstanter utelämnas multiplikationstecknet. Tänk på den berömda ekvationen e=mc 2, vilket föreslår beräkningen av energi som e=m×c 2.
Den verkliga anledningen till att 8÷2(2+2) bröt internet härrör från bruket att utelämna multiplikationssymbolen, som på ett olämpligt sätt fördes till aritmetik från algebra.
Olämplig prioritet
Med andra ord, hade uttrycket "stavats ut" korrekt, det vill säga presenterat som "8 ÷ 2 × (2 + 2) =?", skulle det inte bli viralt, ingen dualitet, inget trasigt internet, inga hetsiga debatter. Inte kul!
I slutändan inbjuder utelämnande av multiplikationssymbolen olämplig prioritet till multiplikation. Alla kommentatorer var överens om att det var det lämpliga första steget att lägga till termerna inom parentes eller parentes. Men förvirring uppstod med tanke på närheten av 2 till (4) i förhållande till 8 i 8÷2(4).
Vi vill veta att det är olämpligt att skriva 2(4) för att hänvisa till multiplikation, men vi förstår att det görs hela tiden och överallt.
Trevlig symbol för multiplikation
Det finns en väldigt fin symbol för multiplikation, så låt oss använda den:2 × 4. Skulle du inte vara ett fan finns det andra symboler, som 2•4. Använd endera, efter eget nöje, men utelämna inte.
Som sådan är debatten om ett mot 16 nu över! Svaret är 16. Ärendet avslutat. Dessutom borde det aldrig ha varit en debatt i första hand. + Utforska vidare
Den här artikeln är återpublicerad från The Conversation under en Creative Commons-licens. Läs originalartikeln. 